Post#1: Factoring Polynomials
To factor the GCF out of a polynomial, we do the following:😉😊
Find the GCF of all the terms in the polynomial.
Express each term as a product of the GCF and another factor.
Use the distributive property to factor out the GCF.
The greatest common factor (GCF) of a set of numbers is the largest factor that all the numbers share. For example, 12, 20, and 24 have two common factors: 2 and 4. The largest is 4, so we say that the GCF of 12, 20, and 24 is 4. GCF is often used to find common denominators.
Factor expressions, also known as factoring, mean rewriting the expression as the product of factors. For example, 3x + 12y can be factored into a simple expression of 3 (x + 4y). In this way, the calculations become easier. The terms 3 and (x + 4y) are known as factors.
The key to factoring is that every term in the trinomial needs to share the factor being taken out. Any factor that's shared by all the terms is called a common factor, and the factor that consists of everything which is shared by all of them is known as the greatest
Example 1. Find the GCF of the following terms: 18 x^ y, 24 x^2 y ^3 , 36 x ^4 y ^2 . The GCF is the product of the factors that appear in each number. At least one 2 and one 3 are factors of each number, so the GCF is 2 ⋅ 3 = 6
The revenue of a company is the amount of money the company receives for selling a product. Say the revenue of a company that sells video games, in thousands of dollars, is: R(x)=−x^2 +400x
, where x is the number of products sold. Being able to factor this function can help us determine when the company has $0 in revenue, as we will see in the next chapter. We start to factor expressions in this section.
The exponents on the x’s are 8, 7, and 6. We have to decide which exponent we are going to use. If we use the exponent 8, we are in trouble. We cannot divide ![]() or
or ![]() by
by ![]() , we don’t have enough x’s to do that. But, if we use
, we don’t have enough x’s to do that. But, if we use ![]() , we would have a monomial that we could divide out of ALL the terms.
, we would have a monomial that we could divide out of ALL the terms.
Hence our GCF is ![]() .
.
Note that if all terms have the same variable, the GCF for the variable part is that variable raised to the lowest exponent that is listed.
Let’s first look at the numerical part. We have a 3, 9, and 18. The largest number that can be divided out of those numbers is 3.
So our numerical GCF is 3.
Now onto the variable part. It looks like each term has an x and a y. In both cases the lowest exponent is 1.
So the GCF of our variable part is xy.
Putting this together we have a GCF of 3xy.
Factoring out the GCF
Step 2: Divide the GCF out of every term of the polynomial.
 Example 3: Factor out the GCF:
Example 3: Factor out the GCF:
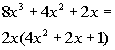
*Divide 2x out of every term of the poly.
Note that if we multiply our answer out, we should get the original polynomial. In this case, it does check out. Factoring gives you another way to write the expression so it will be equivalent to the original problem.

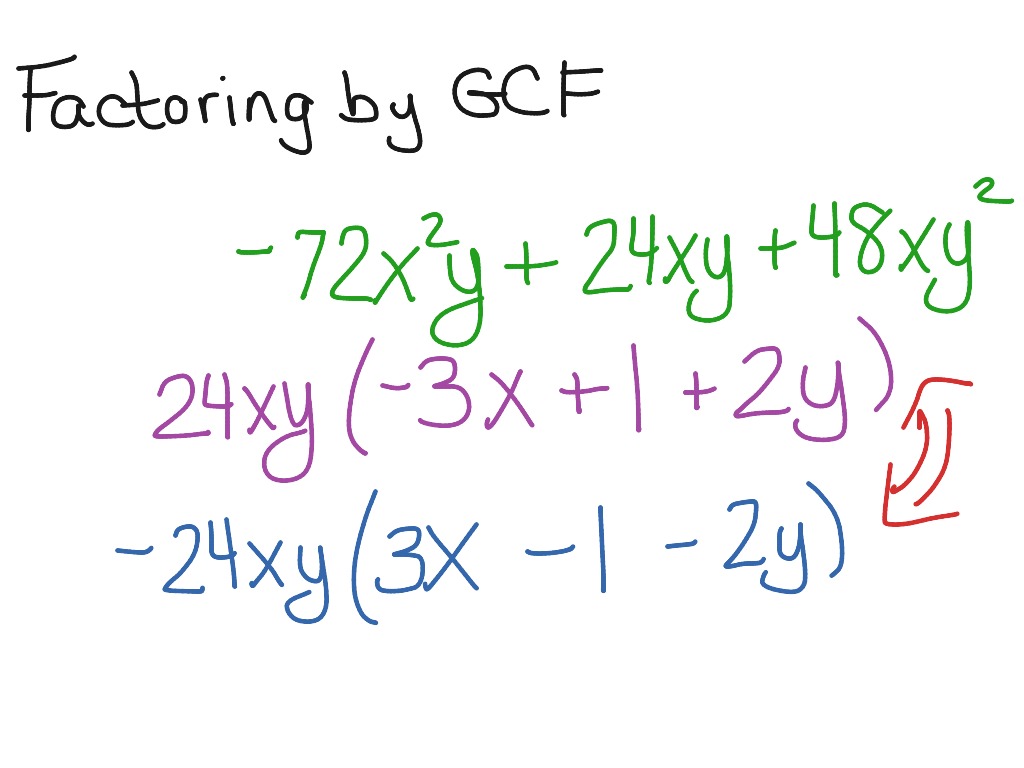


Comments
Post a Comment