Example 4: Factor by grouping: 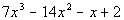 .
.
 View a video of this example
View a video of this example
Note how there is not a GCF for ALL the terms. So let’s go ahead and factor this by grouping.
Step 1: Group the first two terms together and then the last two terms together.
*Two groups of two terms
Be careful. When the first term of the second group of two has a minus sign in front of it, you want to put the minus in front of the second ( ). When you do this you need to change the sign of BOTH terms of the second ( ) as shown above.
Step 2: Factor out a GCF from each separate binomial.
*Factor out a 7x squared from the 1st ( )
*Nothing to factor out from the 2nd ( )
Step 3: Factor out the common binomial.
*Divide (x - 2) out of both parts
Note that if we multiply our answer out that we do get the original polynomial.
Factoring Trinomials of the Form 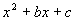
(Where the number in front of x squared is 1)
Basically, we are reversing the FOIL method to get our factored form. We are looking for two binomials that when you multiply them you get the given trinomial.
Step 1: Set up a product of two ( ) where each will hold two terms.
It will look like this: ( )( ).
Step 2: Find the factors that go in the first positions.
To get the x squared (which is the F in FOIL), we would have to have an x in the first positions in each ( ).
So it would look like this: (x )(x ).
Step 3: Find the factors that go in the last positions.
The factors that would go in the last position would have to be two expressions such that their product equals c (the constant) and at the same time their sum equals b (number in front of x term).
As you are finding these factors, you have to consider the sign of the expressions:
If c is positive, your factors are going to both have the same sign depending on b’s sign.
If c is negative, your factors are going to have opposite signs depending on b’s sign.
 Example 5: Factor the trinomial:
Example 5: Factor the trinomial: 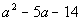 .
.
 View a video of this example
View a video of this example
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the form 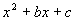 .
.
Step 1: Set up a product of two ( ) where each will hold two terms.
It will look like this: ( )( )
Step 2: Find the factors that go in the first positions.
Since we have a squared as our first term, we will need the following:
(a )(a )
Step 3: Find the factors that go in the last positions.
We need two numbers whose product is -14 and sum is -5. That would have to be -7 and 2.
Putting that into our factors we get:
*-7 and 2 are two numbers whose prod. is -14
and sum is -5
Note that if we would multiply this out, we would get the original trinomial.
 Example 6: Factor the trinomial:
Example 6: Factor the trinomial: 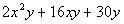 .
.
 View a video of this example
View a video of this example
Note that this trinomial does have a GCF of 2y.
We need to factor out the GCF before we tackle the trinomial part of this.
*Factor out the GCF of 2y
We are not finished, we can still factor the trinomial. It is of the form
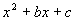
.
Anytime you are factoring, you need to make sure that you factor everything that is factorable. Sometimes you end up having to do several steps of factoring before you are done.
Step 1 (trinomial): Set up a product of two ( ) where each will hold two terms.
It will look like this: 2y( )( )
Step 2 (trinomial): Find the factors that go in the first positions.
Since we have x squared as our first term, we will need the following:
2y(x )(x )
Step 3 (trinomial): Find the factors that go in the last positions.
We need two numbers whose product is 15 and sum is 8. That would have to be 5 and 3.
Putting that into our factors we get:
*5 and 3 are two numbers whose prod. is 15
*and sum is 8
Note that if we would multiply this out, we would get the original trinomial.
Factoring Trinomials of the Form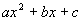
(where a does not equal 1)
Again, this is the reverse of the FOIL method.
The difference between this trinomial and the one discussed above, is there is a number other than 1 in front of the x squared. This means, that not only do you need to find factors of c, but also a.
Step 1: Set up a product of two ( ) where each will hold two terms.
It will look like this ( )( )
Step 2: Use trial and error to find the factors needed.
The factors of a will go in the first terms of the binomials and the factors of c will go in the last terms of the binomials.
The trick is to get the right combination of these factors. You can check this by applying the FOIL method. If your product comes out to be the trinomial you started with, you have the right combination of factors. If the product does not come out to be the given trinomial, then you need to try again.
 Example 7: Factor the trinomial
Example 7: Factor the trinomial 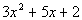 .
.
 View a video of this example
View a video of this example
Note that this trinomial does not have a GCF.
So we go right into factoring the trinomial of the form 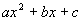 .
.
Step 1: Set up a product of two ( ) where each will hold two terms.
It will look like this: ( )( )
Step 2: Use trial and error to find the factors needed.
In the first terms of the binomials, we need factors of 3 x squared. This would have to be 3x and x.
In the second terms of the binomials, we need factors of 2. This would have to be 2 and 1. I used positives here because the middle term is positive.
Also, we need to make sure that we get the right combination of these factors so that when we multiply them out we get 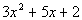 .
.
Possible Factor Check using the FOIL Method First try: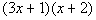
![]() .
.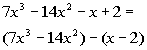
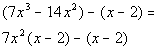
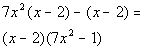
![]()
 Example 5: Factor the trinomial:
Example 5: Factor the trinomial: ![]() .
.![]() .
. Example 6: Factor the trinomial:
Example 6: Factor the trinomial: ![]() .
.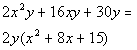
![]()
 Example 7: Factor the trinomial
Example 7: Factor the trinomial ![]() .
.![]() .
.![]() .
.
Comments
Post a Comment